How to Read an Input File of a Graph in C

4.ane   Undirected Graphs

Graphs.

A graph is a set of vertices and a collection of edges that each connect a pair of vertices. Nosotros use the names 0 through V-1 for the vertices in a V-vertex graph.

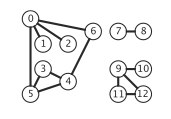
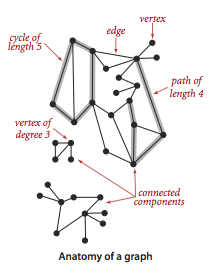
Glossary.

Here are some definitions that we apply.

• A cocky-loop is an edge that connects a vertex to itself.
• Two edges are parallel if they connect the same pair of vertices.
• When an edge connects 2 vertices, we say that the vertices are side by side to ane another and that the edge is incident on both vertices.
• The caste of a vertex is the number of edges incident on information technology.
• A subgraph is a subset of a graph'south edges (and associated vertices) that constitutes a graph.
• A path in a graph is a sequence of vertices connected past edges, with no repeated edges.
• A simple path is a path with no repeated vertices.
• A bike is a path (with at least one edge) whose first and terminal vertices are the same.
• A simple cycle is a cycle with no repeated vertices (other than the requisite repetition of the first and last vertices).
• The length of a path or a bike is its number of edges.
• We say that 1 vertex is connected to another if there exists a path that contains both of them.
• A graph is connected if in that location is a path from every vertex to every other vertex.
• A graph that is non continued consists of a set of connected components, which are maximal connected subgraphs.
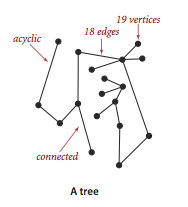
• An acyclic graph is a graph with no cycles.
• A tree is an acyclic connected graph.
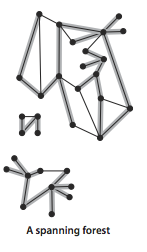
• A forest is a disjoint set up of copse.
• A spanning tree of a continued graph is a subgraph that contains all of that graph'due south vertices and is a single tree. A spanning forest of a graph is the union of the spanning trees of its connected components.
• A bipartite graph is a graph whose vertices we tin can divide into two sets such that all edges connect a vertex in one set with a vertex in the other set.

Undirected graph data type.

Nosotros implement the following undirected graph API.

The cardinal method adj() allows customer code to iterate through the vertices next to a given vertex. Remarkably, we can build all of the algorithms that we consider in this department on the basic abstraction embodied in adj().

Nosotros prepare the test data tinyG.txt, mediumG.txt, and largeG.txt, using the following input file format.

GraphClient.java contains typical graph-processing code.

Graph representation.

We use the adjacency-lists representation, where we maintain a vertex-indexed assortment of lists of the vertices connected by an edge to each vertex.

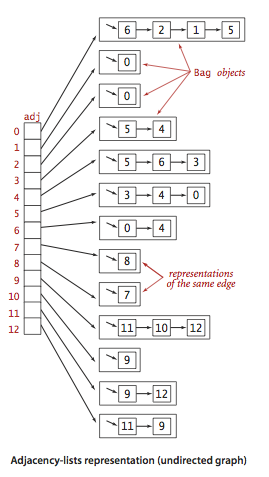
Graph.java implements the graph API using the adjacency-lists representation. AdjMatrixGraph.java implements the same API using the adjacency-matrix representation.

Depth-first search.

Depth-beginning search is a classic recursive method for systematically examining each of the vertices and edges in a graph. To visit a vertex

• Marker it as having been visited.
• Visit (recursively) all the vertices that are adjacent to it and that have not still been marked.

DepthFirstSearch.java implements this arroyo and the post-obit API:

Finding paths.

It is like shooting fish in a barrel to change depth-start search to not only decide whether there exists a path between two given vertices but to discover such a path (if ane exists). We seek to implement the following API:

To accomplish this, we recollect the edge v-w that takes united states of america to each vertex westward for the first time by setting edgeTo[due west] to five. In other words, v-westward is the terminal edge on the known path from s to w. The result of the search is a tree rooted at the source; edgeTo[] is a parent-link representation of that tree. DepthFirstPaths.java implements this approach.

Latitude-first search.

Depth-offset search finds some path from a source vertex s to a target vertex v. We are frequently interested in finding the shortest such path (one with a minimal number of edges). Breadth-first search is a classic method based on this goal. To find a shortest path from

s

to

v

, we start at

s

and check for

v

amongst all the vertices that we tin can accomplish by following one border, and then we check for

five

among all the vertices that nosotros tin reach from

s

by post-obit two edges, and and so forth.

To implement this strategy, nosotros maintain a queue of all vertices that have been marked but whose adjacency lists have not been checked. Nosotros put the source vertex on the queue, and then perform the post-obit steps until the queue is empty:

• Remove the next vertex v from the queue.
• Put onto the queue all unmarked vertices that are next to five and marking them.

BreadthFirstPaths.java is an implementation of the

Paths

API that finds shortest paths. Information technology relies on Queue.coffee for the FIFO queue.

Connected components.

Our next direct application of depth-first search is to find the connected components of a graph. Recollect from Section one.5 that "is connected to" is an equivalence relation that divides the vertices into equivalence classes (the connected components). For this task, nosotros define the following API:

CC.java uses DFS to implement this API.

Suggestion. DFS marks all the vertices connected to a given source in time proportional to the sum of their degrees and provides clients with a path from a given source to any marked vertex in time proportional to its length.

Proposition. For any vertex 5 reachable from due south, BFS computes a shortest path from due south to 5 (no path from s to v has fewer edges). BFS takes time proportional to V + E in the worst case.

Suggestion. DFS uses preprocessing fourth dimension and infinite proportional to V + Due east to support constant-time connectivity queries in a graph.

More than depth-commencement search applications.

The bug that we have solved with DFS are fundamental. Depth-showtime search can also be used to solve the post-obit problems:

• Cycle detection: Is a given graph acyclic? Cycle.java uses depth-first search to determine whether a graph has a wheel, and if so return one. It takes time proportional to V + E in the worst case.
• Two-colorability: Can the vertices of a given graph be assigned one of two colors in such a way that no border connects vertices of the aforementioned color? Bipartite.java uses depth-first search to decide whether a graph has a bipartition; if then, render one; if not, return an odd-length cycle. It takes time proportional to V + E in the worst case.
• Bridge: A bridge (or cut-edge) is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. Bridge.java uses depth-first search to discover fourth dimension the bridges in a graph. Information technology takes time proportional to V + East in the worst case.
• Biconnectivity: An articulation vertex (or cutting vertex) is a vertex whose removal increases the number of continued components. A graph is biconnected if it has no joint vertices. Biconnected.java uses depth-outset search to find the bridges and joint vertices. It takes time proportional to V + Eastward in the worst case.
• Planarity: A graph is planar if it tin can be drawn in the aeroplane such that no edges cross 1 another. The Hopcroft-Tarjan algorithm is an avant-garde awarding of depth-kickoff search that determines whether a graph is planar in linear fourth dimension.

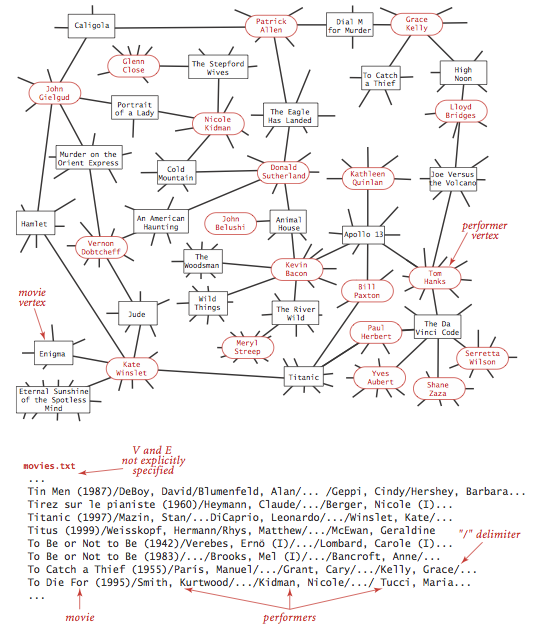
Symbol graphs.

Typical applications involve processing graphs using strings, not integer indices, to ascertain and refer to vertices. To accommodate such applications, nosotros define an input format with the following properties:

• Vertex names are strings.
• A specified delimiter separates vertex names (to allow for the possibility of spaces in names).
• Each line represents a ready of edges, connecting the first vertex proper noun on the line to each of the other vertices named on the line.

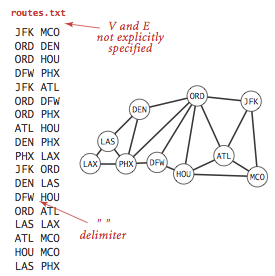
The input file routes.txt is a pocket-size example.

The input file movies.txt is a larger case from the Internet Movie Database. This file consists of lines list a movie name followed by a list of the performers in the motion-picture show.

• API. The following API allows united states of america to utilise our graph-processing routines for such input files.

  

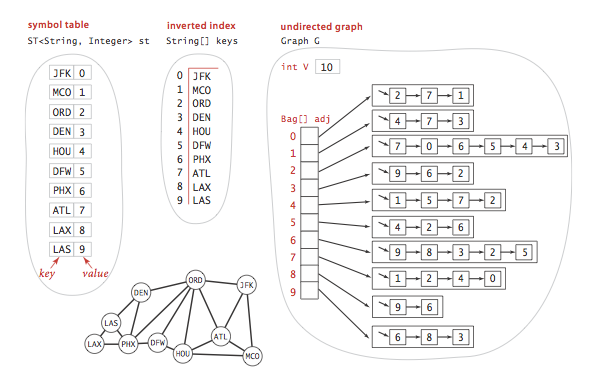
• Implementation. SymbolGraph.java implements the API. It builds three data structures:
  • A symbol table st with String keys (vertex names) and int values (indices)
  • An array keys[] that serves as an inverted alphabetize, giving the vertex name associated with each integer alphabetize
  • A Graph Thou built using the indices to refer to vertices

  

• Degrees of separation. DegreesOfSeparation.java uses breadth-get-go search to find the caste of separation between 2 individuals in a social network. For the actor-movie graph, information technology plays the Kevin Salary game.

Exercises

3. Create a copy constructor for Graph.java that takes as input a graph G and creates and initializes a new copy of the graph. Any changes a client makes to Grand should not affect the newly created graph.
13. Add together a distTo() method to BreadthFirstPaths.java, which returns the number of edges on the shortest path from the source to a given vertex. A distTo() query should run in constant time.
23. Write a programme BaconHistogram.java that prints a histogram of Kevin Salary numbers, indicating how many performers from movies.txt have a Bacon number of 0, ane, 2, iii, ... . Include a category for those who have an infinite number (not connected to Kevin Bacon).
26. Write a SymbolGraph client DegreesOfSeparationDFS.java that uses depth-first instead of breadth-first search to find paths connecting two performers.
27. Decide the amount of retentiveness used by Graph to represent a graph with 5 vertices and East edges, using the memory-cost model of Department 1.four.

    Solution. 56 + 40V + 128E. MemoryOfGraph.java computes it empirically assuming that no Integer values are cached—Java typically caches the integers -128 to 127.

Artistic Bug

32. Parallel edge detection. Devise a linear-time algorithm to count the parallel edges in a graph.

    Hint: maintain a boolean array of the neighbors of a vertex, and reuse this array past simply reinitializing the entries as needed.

36. Two-border connectivity. A bridge in a graph is an border that, if removed, would separate a continued graph into two disjoint subgraphs. A graph that has no bridges is said to be two-edge connected. Develop a DFS-based data type Bridge.java for determining whether a given graph is edge continued.

Spider web Exercises

1. Find some interesting graphs. Are they directed or undirected? Sparse or dense?
2. Degree. The degree of a vertex is the number of incident edges. Add a method int caste(int 5) to Graph that returns the caste of the vertex v.
3. Suppose you apply a stack instead of a queue when running latitude-first search. Does it still compute shortest paths?
4. DFS with an explicit stack. Requite an example of possibility of stack overflow with DFS using the function call stack, e.1000., line graph. Modify DepthFirstPaths.java and so that it uses an explicit stack instead of the function call stack.
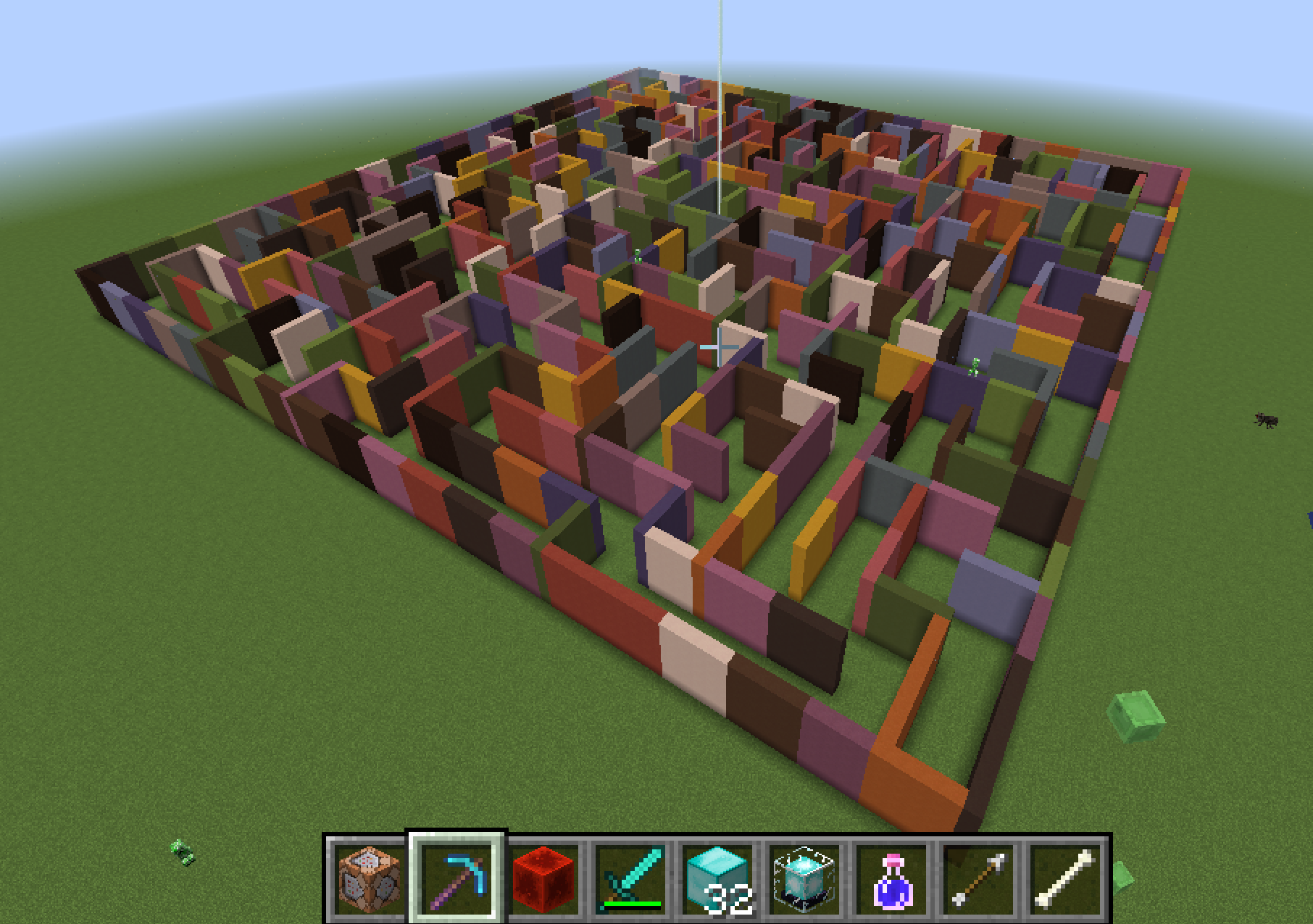
5. Perfect maze. Generate a perfect maze similar this one

   Write a program Maze.coffee that takes a command-line argument n, and generates a random n-by-n perfect maze. A maze is perfect if information technology has exactly one path between every pair of points in the maze, i.e., no inaccessible locations, no cycles, and no open up spaces. Here's a nice algorithm to generate such mazes. Consider an n-by-n filigree of cells, each of which initially has a wall between it and its four neighboring cells. For each prison cell (x, y), maintain a variable north[x][y] that is truthful if there is wall separating (10, y) and (ten, y + ane). We accept analogous variables east[x][y], south[x][y], and w[ten][y] for the corresponding walls. Note that if there is a wall to the north of (ten, y) so northward[x][y] = south[ten][y+one] = true. Construct the maze by knocking down some of the walls as follows:

   1. Commencement at the lower level jail cell (1, ane).
   2. Find a neighbor at random that you haven't yet been to.
   3. If you find i, move there, knocking downwardly the wall. If you don't observe one, become dorsum to the previous cell.
   4. Repeat steps ii. and three. until you've been to every cell in the filigree.

   Hint: maintain an (n+2)-by-(n+ii) filigree of cells to avert dull special cases.

   Hither is a Mincecraft maze created by Carl Eklof using this algorithm.

   

6. Getting out of the maze. Given an due north-by-n maze (like the one created in the previous practise), write a program to find a path from the showtime cell (i, 1) to the stop jail cell (n, n), if it exists. To find a solution to the maze, run the following algorithm, starting from (1, ane) and stopping if we reach prison cell (due north, northward).

   explore(10, y) -------------   - Marking the electric current cell (x, y) equally "visited."   - If no wall to north and unvisited, then explore(ten, y+one).   - If no wall to eastward and  unvisited, then explore(x+1, y).   - If no wall to south and unvisited, then explore(10, y-one).   - If no wall to westward and  unvisited, and then explore(ten-one, y).                

7. Maze game. Develop a maze game like this one from gamesolo.com, where you traverse a maze, collecting prizes.
8. Actor graph. An alternate (and perhaps more natural) way to compute Kevin Bacon numbers is to build a graph where each node is an actor. Two actors are connected by an border if they appear in a moving picture together. Calculate Kevin Bacon numbers by running BFS on the actor graph. Compare the running time versus the algorithm described in the text. Explicate why the arroyo in the text is preferable. Respond: it avoids multiple parallel edges. As a result, it's faster and uses less memory. Moreover, it's more than user-friendly since you don't accept to characterization the edges with the movie names - all names get stored in the vertices.
9. Middle of the Hollywood universe. Nosotros can mensurate how practiced of a eye that Kevin Bacon is past calculating their Hollywood number. The Hollywood number of Kevin Bacon is the average Bacon number of all the actors. The Hollywood number of another actor is computed the aforementioned fashion, but we make them be the source instead of Kevin Bacon. Compute Kevin Bacon's Hollywood number and find an actor and actress with better Hollywood numbers.
10. Fringe of the Hollywood universe. Discover the actor (who is connected to Kevin Bacon) that has the highest Hollywood number.
11. Word ladders. Write a program WordLadder.java that takes two 5 letter strings from the command line, and reads in a list of 5 letter words from standard input, and prints out a shortest give-and-take ladder connecting the ii strings (if it exists). Two words can be connected in a word ladder chain if they differ in exactly one letter. Equally an example, the post-obit word ladder connects green and brown.

    green greet great groat groan grown chocolate-brown                

    You can also try out your program on this listing of 6 letter words.

12. Faster give-and-take ladders. To speed things upwards (if the word list is very big), don't write a nested loop to try all pairs of words to see if they are next. To handle 5 letter words, first sort the word listing. Words that simply differ in their last letter of the alphabet will appear consecutively in the sorted list. Sort 4 more times, but cyclically shift the messages one position to the right and then that words that differ in the ith letter volition appear consecutively in one of the sorted lists.

    Endeavor out this approach using a larger word list with words of different sizes. Two words of different lengths are neighbors if the smaller word is the same as the bigger word, minus the last alphabetic character, due east.yard., forehead and brown.

13. Suppose yous delete all of the bridges in an undirected graph. Are the connected components of the resulting graph the biconnected components? Answer: no, two biconnected components tin exist connected through an articulation indicate.

    Bridges and articulation points.

    A bridge (or cutting edge) is an edge whose removal disconnects the graph. An articulation point (or cutting vertex) is a vertex whose removal (and removal of all incident edges) disconnects the remaining graph. Bridges and articulations points are important considering they correspond a single indicate of failure in a network. Brute strength: delete edge (or vertex) and check connectivity. Takes O(Due east(V + Eastward)) and O(V(V + E)) time, respectively. Can amend both to O(East + V) using clever extension to DFS.
14. Biconnected components. An undirected graph is biconnected if for every pair of vertices v and w, there are two vertex-disjoint paths between v and w. (Or equivalently a elementary cycle through any two vertices.) Nosotros define a cocyclicity equivalence relation on the edges: two edges e1 and e2 are are in same biconnected component if e1 = e2 or there exists a wheel containing both e1 and e2. Two biconnected components share at nigh one vertex in common. A vertex is an articulation bespeak if and only if it is mutual to more than than one biconnected component. Programme Biconnected.java identifies the bridges and articulation points.
15. Biconnected components. Modify Biconnected to print out the edges that constitute each biconnected component. Hint: each bridge is its own biconnected component; to compute the other biconnected components, mark each joint bespeak as visited, and then run DFS, keeping rail of the edges discovered from each DFS showtime betoken.
16. Perform numerical experiments on the number of connected components for random undirected graphs. Phase change around 1/ii V ln V. (Run across Belongings 18.thirteen in Algs Java.)
17. Rogue. (Andrew Appel.) A monster and a actor are each located at a distinct vertex in an undirected graph. In the role playing game Rogue, the player and the monster alternate turns. In each plough the thespian can move to an adjacent vertex or stays put. Decide all vertices that the player can reach before the monster. Assume the player gets the first move.
18. Rogue. (Andrew Appel.) A monster and a thespian are each located at a distinct vertex in an undirected graph. The goal of the monster is to land on the same vertex equally the player. Devise an optimal strategy for the monster.
19. Articulation point. Let G be a connected, undirected graph. Consider a DFS tree for Yard. Evidence that vertex v is an articulation point of G if and merely if either (i) 5 is the root of the DFS tree and has more than than one child or (ii) v is not the root of the DFS tree and for some child w of v there is no dorsum edge between any descendant of west (including w) and a proper ancestor of v. In other words, v is an articulation bespeak if and only if (i) 5 is the root and has more than ane child or (ii) v has a kid west such that low[w] >= pre[v].
20. Sierpinski gasket. Nice example of an Eulerian graph.
21. Preferential zipper graphs. Create a random graph on V vertices and E edges equally follows: kickoff with V vertices v1, .., vn in any order. Pick an chemical element of sequence uniformly at random and add to end of sequence. Repeat 2E times (using growing list of vertices). Pair up the final 2E vertices to form the graph.

    Roughly speaking, it's equivalent to calculation each edge one-by-i with probability proportional to the product of the degrees of the two endpoints. Reference.

22. Wiener index. The Wiener index of a vertex is the sum of the shortest path distances between v and all other vertices. The Wiener alphabetize of a graph Grand is the sum of the shortest path distances over all pairs of vertices. Used by mathematical chemists (vertices = atoms, edges = bonds).
23. Random walk. Like shooting fish in a barrel algorithm for getting out of a maze (or st connectivity in a graph): at each stride, take a step in a random direction. With consummate graph, takes V log 5 fourth dimension (coupon collector); for line graph or cycle, takes Five^2 time (gambler's ruin). In general the encompass time is at most 2E(V-one), a classic result of Aleliunas, Karp, Lipton, Lovasz, and Rackoff.
24. Deletion order. Given a continued graph, determine an gild to delete the vertices such that each deletion leaves the (remaining) graph connected. Your algorithm should take fourth dimension proportional to Five + East in the worst case.
25. Center of a tree. Given a graph that is a tree (continued and acyclic), find a vertex such that its maximum altitude from any other vertex is minimized.

    Hint: find the diameter of the tree (the longest path betwixt ii vertices) and return a vertex in the middle.

26. Diameter of a tree. Given a graph that is a tree (connected and acyclic), find the longest path, i.e., a pair of vertices 5 and westward that are as far apart as possible. Your algorithm should run in linear time.

    Hint. Pick whatsoever vertex v. Compute the shortest path from v to every other vertex. Let westward be the vertex with the largest shortest path distance. Compute the shortest path from due west to every other vertex. Let 10 be the vertex with the largest shortest path distance. The path from w to x gives the diameter.

27. Bridges with matrimony-find. Permit T exist a spanning tree of a continued graph G. Each non-tree edge e in G forms a primal cycle consisting of the border due east plus the unique path in the tree joining its endpoings. Prove that an border is a bridge if and simply if it is non on some fundamental bike. Thus, all bridges are edges of the spanning tree. Pattern an algorithm to find all of the bridges (and bridge components) using E + V time plus Eastward + V union-find operations.
28. Nonrecursive depth-first search. Write a program NonrecursiveDFS.java that implements depth-first search with an explicit stack instead of recursion.

    Hither is an alternating implementation suggested by Bin Jiang in the early 1990s. The merely extra memory is for a stack of vertices but that stack must support arbitrary deletion (or at least the motion of an capricious item to the tiptop of the stack).

    private void dfs(Graph Thousand, int southward) {     SuperStack<Integer> stack = new SuperStack<Integer>();     stack.push(s);     while (!stack.isEmpty()) {         int v = stack.peek();         if (!marked[v]) {             marked[v] = true;             for (int w : G.adj(v)) {                 if (!marked[west]) {                     if (stack.contains(due west)) stack.delete(w);                     stack.push(w);                 }             }         }         else {             // v'south adjacency listing is exhausted             stack.pop();         }     } }                

    Hither is yet another implementation. Information technology is, perchance, the simplest nonrecursive implementation, just it uses space proportional to E + V in the worst case (because more than one copy of a vertex can be on the stack) and it explores the vertices adjacent to v in the reverse order of the standard recursive DFS. Also, an edgeTo[v] entry may be updated more than once, so it may not be suitable for backtracking applications.

    private void dfs(Graph Chiliad, int due south) {     Stack<Integer> stack = new Stack<Integer>();     stack.button(s);     while (!stack.isEmpty()) {         int v = stack.popular();         if (!marked[v]) {             marked[v] = true;             for (int w : G.adj(v)) {                 if (!marked[west]) {                     edgeTo[w] = v;                     stack.push(w);                  }             }         }     } }                

29. Nonrecursive depth-first search. Explan why the following nonrecursive method (coordinating to BFS but using a stack instead of a queue) does not implement depth-first search.

    private void dfs(Graph G, int south) {     Stack<Integer> stack = new Stack<Integer>();     stack.push(s);     marked[s] = true;     while (!stack.isEmpty()) {        int five = stack.popular();        for (int w : Yard.adj(v)) {            if (!marked[w]) {                stack.push(west);                marked[w] = true;                edgeTo[w] = five;            }        }     } }                

    Solution: Consider the graph consisting of the edges 0-i, 0-2, 1-2, and 2-i, with vertex 0 equally the source.

30. Matlab continued components. bwlabel() or bwlabeln() in Matlab characterization the connected components in a 2nd or kD binary image. bwconncomp() is newer version.
31. Shortest path in complement graph. Given a graph G, design an algorithm to find the shortest path (number of edges) between s and every other vertex in the complement graph Yard'. The complement graph contains the same vertices every bit G but includes an border 5-w if and merely if the border v-w is not in M. Tin can you practice any improve than explicitly computing the complement graph G' and running BFS in Yard'?
32. Delete a vertex without disconnecting a graph. Given a connected graph, design a linear-time algorithm to detect a vertex whose removal (deleting the vertex and all incident edges) does not disconnect the graph.

    Hint 1 (using DFS): run DFS from some vertex s and consider the first vertex in DFS that finishes.

    Hint two (using BFS): run BFS from some vertex s and consider any vertex with the highest distance.

33. Spanning tree. Design an algorithm that computes a spanning tree of a connected graph is time proportional to V + Eastward. Hint: use either BFS or DFS.
34. All paths in a graph. Write a programme AllPaths.coffee that enumerates all elementary paths in a graph betwixt 2 specified vertices. Hint: use DFS and backtracking. Alarm: there many be exponentially many unproblematic paths in a graph, so no algorithm tin can run efficiently for large graphs.

gilesplis1938.blogspot.com

Source: https://algs4.cs.princeton.edu/41graph/

Share this post